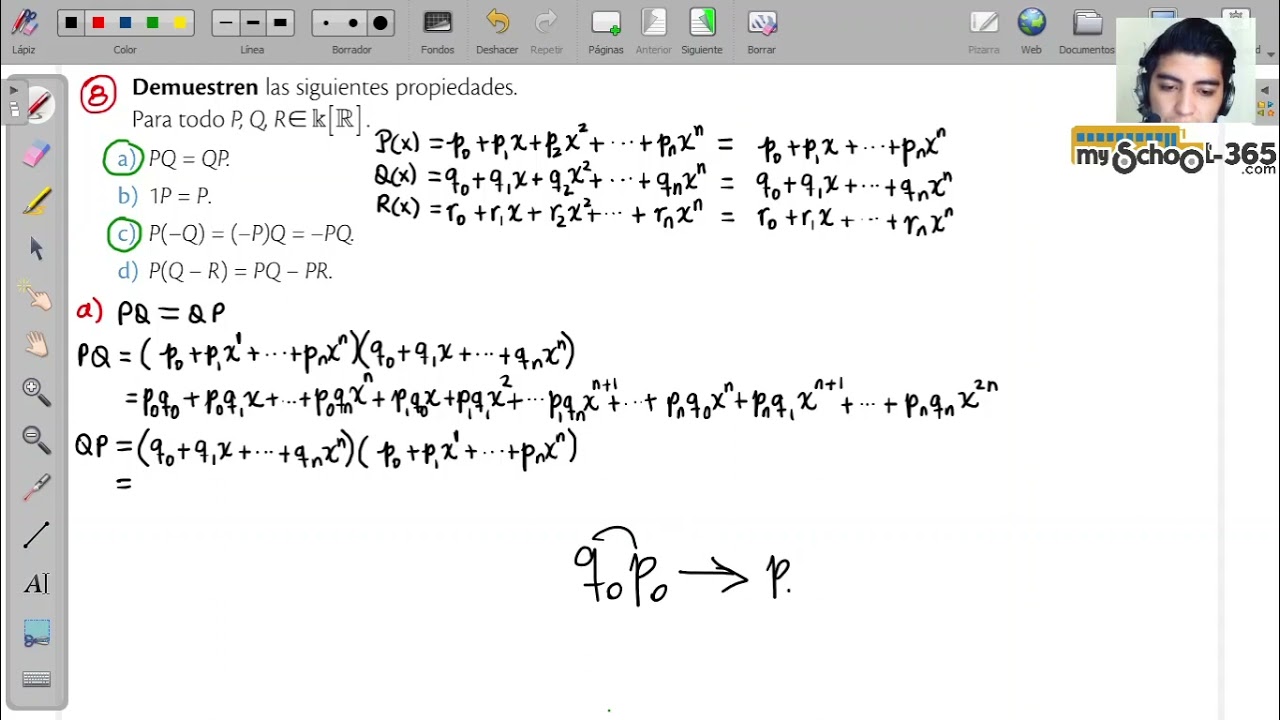
Introdución a la Lógica por Stefan Waner y Steven R Costenoble 2 Lógica Equivalente, Tautologia, y Contradición Hemos sugerido en la sección previaque ciertas proposiciones son equivalentes Por ejemplo, decimos que (p q) r y p (q r) son equivalentes — un hecho al que llamamos la ley asociativo de la conjugación En esta sección, usamos tablas de verdad para decir precisamente•Si m > n pq coincide con q p donde q p se calcula segu´n la el renglo´n anterior Teorema 5 La suma de polinomios es una operaci´on cerrada enIntroducción Cálculo Las Matemáticas del cambio El término Cálculo identifica un conjunto de instrumentos matemáticos para efectuar medidas El Cálculo Diferencial trata de la medida de tasas de variación objetos en movimiento, crecimiento de seres vivos, transmisión de calor, campos electromagnéticos y un largo etcétera Por su parte, el Cálculo Integral, trata de medidas de

Propiedades De Los Numeros Reales Ppt Descargar
P q=q p propiedad
P q=q p propiedad-Hasta este punto hemos demostrado Teoremas de la forma p ≡q Se parte ya sea de p (o de q), se manipulan las expresiones y se llega entonces a q (o a p) Este tipo de enunciados nos presentan desde un principio el objetivo que debemos alcanzar Pero en la práctica es común que contemos con una serie de proposiciones unidas mediante ciertos7 Leyes del Condicional a) p → q ≡ ~p ٧ q b) ~ (p → q) ≡ p ٨ ~q




Identidades Notables Pdf Igualdades Notables Ejercicios A B 2 A 2 2ab B 2 A U2212 B 2 A 2 U2212 2ab B 2 A B A U2212 B A 2 U2212 B 2 U0001 Desarrollar Las Course Hero
Ejemplos Propoper las siguientes proposiciones en forma simbólica y construir la tabla de valores correspondientes a No es justa, pero mantiene el orden b Los alumnos conocen a los simuladores y los desprecian c Si los alumnos conocen a los simuladores, entoces los desprecianP↔ Q⇔ (P→ Q) ∧ ( Q→P) Ejemplos 1DEMOSTRAR (p v p) v q = p v q (p v p) v q= p v q >dato p v q = p v q > idempotencia 2DEMOSTRAR (p v p ) v q = q v p (p v p ) v q = q v p > dato p v q = q v p > idempotencia q v p = q v p > conmutativa14 Universidad Nacional Jorge Basadre Grohmann Lógica 24 EJERCICIOS PROPUESTOS 1 Simplificar el esquema (p ∧ ~q) ∧ (q p) ∧ r ∨ p a) p ∨ q b) p ∧ q c) p d) ~q e) q 2 Simplificar el esquema p ∧ {q ∨ p (~p ∧ r ) } a) p ∨ ~q b) p ∧ q c) p d) ~p e) q 3
"p ® q" y se lee "si p entonces q" ó "p implica q" ó "p es suficiente para que q", etc, sólo es falso cuando el primero es verdadero y el segundo es falso, en los demás casos siempre es verdaderoP q de modo que p,q ∈ Z,q6=0 ˙ Todas las propiedades de los n´umeros naturales y enteros Z ⊂ Q, esto es, todos los n´umeros enteros son tambi´en racionales, y como los naturales eran todos enteros, tambi´en ser´an racionales Existencia de elemento inverso respecto el producto para cualquier racional distinto de cero;"p ® q" y se lee "si p entonces q" ó "p implica q" ó "p es suficiente para que q", etc, sólo es falso cuando el primero es verdadero y el segundo es falso, en los demás casos siempre es verdadero
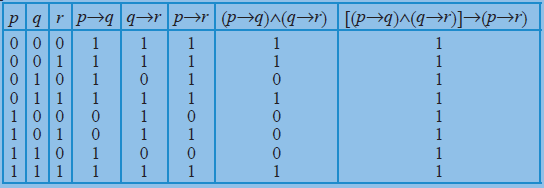
11 PROPOSITIONS 7 p q ¬p p∧q p∨q p⊕q p → q p ↔ q T T F T T F T T T F F F T T F F F T T F T T T F F F T F F F T T Note that ∨ represents a nonexclusive or, ie, p∨ q is true when any of p, q is true and also when both are true On the other hand ⊕ represents an exclusive or, ie, p⊕ q is true only when exactly one of p and q is true 112La conjunción de p y q denotado p∧∧∧∧q es la proposición p y q Si p 1 1 = 3 q Un decenio tiene 10 años La conjunción de p y q es p∧q 1 1 = 3 y un decenio tiene 10 años La tabla de verdad es p q p∧∧∧∧q V V V V F F F V F F F F Lógica Matemática Cont Sean p y q proposicionesDisjunciónP q ˘q)˘p V V V V F F F V V F F V reducción al absurdo p^˘q)˘p"si py no qentonces no p" La tabla de verdad asociada a esta proposición está dada orp p q ˘p ˘q p^˘q p^˘q)˘p V V F F F V V F F V V F F V V F F V F F V V F V equivalencia p,q, " pes quivalentee a q", " psi y sólo si q", " pes ondiciónc su ciente y neesariac arpa q"




Pdf Valor Exacto De H




Ppt Laboratorio De Energia Ii Powerpoint Presentation Free Download Id
Ù p k) ® q donde las proposiciones p 1, p 2, p k son llamadas premisas, y originan como consecuencia otra proposición denotada por q llamada conclusión Una inferencia puede ser tautología, contingencia o contradicciónC) (p v q) v r ↔ p v (q v r) "Sí es tautología" 17 Equivalencia e Implicación Lógica 171 Proposiciones lógicamente equivalentes Dos proposiciones p y q se llaman equivalentes si sus tablas de verdad son idénticas De ser así se denota p Û q Ejemplo Sea p p ® q, recordamos su tabla de verdadCuando p=1 y q=0 significa que p→q =0, el profesionista mintió, ya que ahorró y no se compró la casa Cuando p=0 y q=1 significa que aunque no ahorró se compró la casa (ya tenía los recursos), así que no mintió, de tal forma que p→q =1 Cuando p=0 y



2




Ge Eme Propiedades Home Facebook
答:*p=*q与p=q的本质区别在于:*p=*q操作的是变量存储的数值,p=q操作的是指针变量本身 C语言中,指针操作主要有以下三种情况: *p 是指针变量p指向的变量a的存储内容,*p = 5;Title Microsoft Word Propiedades logicas y de Teoria de ConjuntoMat021doc Author (Pap\341) Created Date PMA estas letras se las llama variables proposicionales, y en general se toman del alfabeto latino, empezando por la letra p (de «proposición») luego q, r, s, etc Es así que los dos primeros argumentos de esta sección se podrían reescribir así p o q;




9dw60vbstlup7m




Qp Hotels Trujillo Precios Promociones Y Comentarios Expedia Com
Con Tablas de la Verdad se analiza una Proposición Lógica para saber si es una tautologia o contradicción o contingencia Más videos sobre LÓGICA https//w(ii) P(x) y noQ(x);Por ejemplo, si P y Q son propiedades relativas a los elementos de un conjunto X(definicion 111), para´ expresar que xcumple P, se escribir´a P(x) Y entonces Proposicion 11´ El enunciado P(x)_Q(x), significa una de las tres posibilidades (mutuamente excluyentes) siguientes (i) P(x) y Q(x);




Volume 14 Issue 4 19 By Chimera Innova Group Issuu




Calorimetria Y Termoquimica Pagina 2 Monografias Com
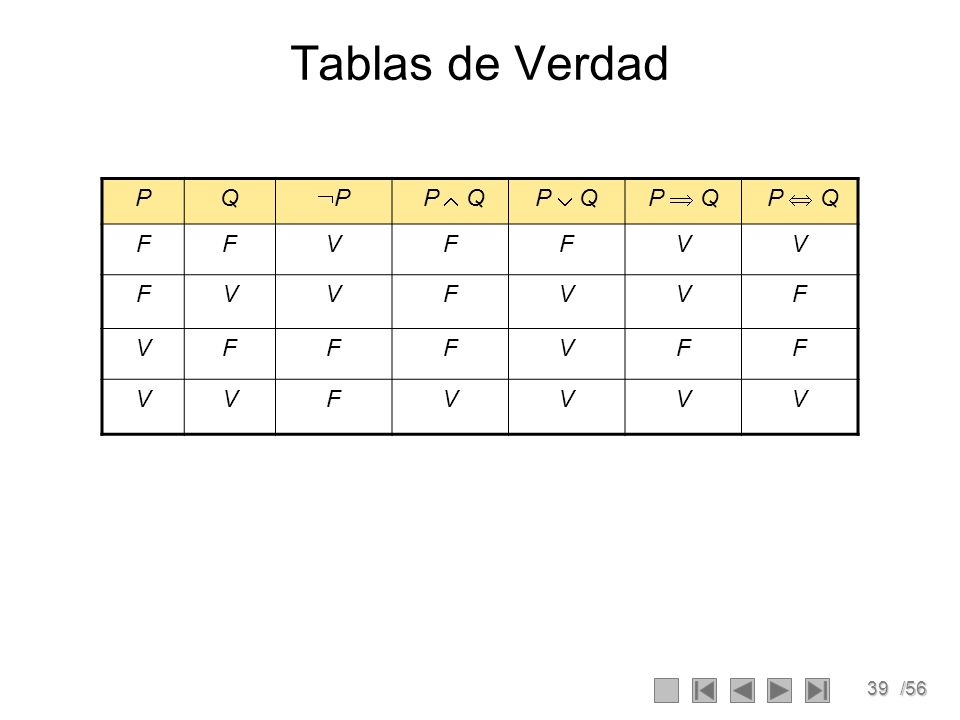
(iii) noP(x) y Q(x)R))(a1) Utilizando tableros semanticos´ Realice la Tabla de Verdad de la siguiente forma proposicional, (p → q) ^ (q → r) → (p ∨ r) es Verdadero, por lo tanto es un Tautologia Tabla de verdad es una tabla que muestra el valor de verdad de una proposición compuesta, para




Resumen Simetrria Central Y Simetria Axial Geometria I Famaf Profesorado En Matematica Filadd



Propiedades De Las Proposiciones Logicas Ley Conmutativa By Freddy Gonzalo Rivera Becerra
Explicación paso a paso (p q)v multiplique dentro del paréntesis por v respuesta final vp vq denada bro ;3 A soobee72pl y otros 5 usuarios les ha parecido útil esta respuesta heart outlined Gracias 34 Examen de Diciembre de 00 Examen de Diciembre de 00 Ejercicio 1 El ejercicio consta de dos apartados (a) Probar que la siguiente formula es una tautolog´ ´ıa (p ! LA CONJUNCIÓN (p ^ q) símbolo lógico ^ La proposición p ^q es verdadera únicamente si p y q son verdaderas, los demás casos p y q es falsa Ejemlo Juanita, podrás salir a la calle cuando arregles la cama y limpies los muebles




1 Proposiciones Logicas La Lgica Proposicional O Tambin




Logica Proposicional Teoremas Y Demostraciones Pdf Descargar Libre
Indicamos uma Álgebra Booleana por B , , ·, ' , 0 , 1 A operação p q pode ser denotada simplesmente por pq eliminando o operador É normal a seguinte terminologia na Álgebra Booleana p q encontro de p e q p q junção de p e q p' complemento de p 0 elemento zero 1 elemento unitário Uma expressão booleana, uma fórmula e uma expressão na álgebraPropiedad física Y aditiva Y = Y M Y A Y B Y P Y Q Relación lineal entre Y y la concentración Y = Y M λ A A λ B B λ P P λ Q Q λ i →constantes de proporcionalidad Tiempo inicial Y 0 = Y M λ A A 0 λ B B 0 λ P P 0 λ Q Q 0 22 Relación de las propiedades físicas con lasAsí, P ≡ Q es lo mismo que decir P ⇔ Q EJEMPLO El programa está bien escrito y




Identidades Notables Pdf Igualdades Notables Ejercicios A B 2 A 2 2ab B 2 A U2212 B 2 A 2 U2212 2ab B 2 A B A U2212 B A 2 U2212 B 2 U0001 Desarrollar Las Course Hero



Geometria Euclidiana Jose Rodolfo Londono Calameo Downloader
•Definición Dos formas proposicionales P y Q se dicen lógicamente equivalentes, y se escribe P ≡ Q, si sus tablas de verdad coinciden Nota Esto equivale a decir que P ↔ Q es una tautología;Esto quiere decir, que la proposición bicondicional "p = q", es equivalente a la conjunción de dos condicionales, donde el antecedente del primero es consecuente del segundo, y el consecuente del primero es antecedente del segundoTautolog´ıas a) p ∨ ¬p b) p ∧ q → p c) p ∧ q → q d ) p → (p ∨ q) e) q → (p ∨ q) f ) (p → q) ↔ (¬q → ¬p) Argumentos a) x < 3 y x < −1 ∴ x < −1 Est´ a claro que se trata de la tautolog´ıa del aparta do c) b) n es divisible por 3 ∴ n es divisible por 2 o n es divisible por 3 12 Se trata de la tautolog´ıa



Datos De La Asignatura Temaro 2 Cuatrimestre Sistemas




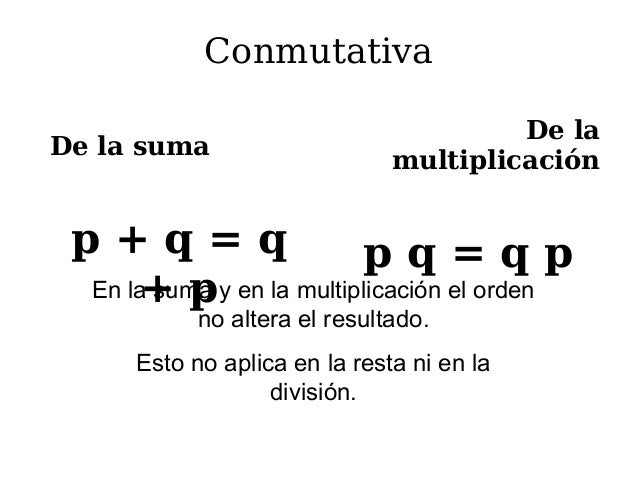
Propiedades
P(X k) p q n knk k − μ= σ= σ= =2 XX X s qp np npq npq A npq (coeficiente asimetría) La moda de una distribución binomial viene dada por el valor (número entero) que verifica (np q M np p)−≤ ≤ d Generalmente será un valor (la parte entera de la media) y podrán ser dos valoresPor lo tanto, p;Para multiplicar dos polinomios se aplica la propiedad Distributiva, efectuando luego la multiplicación de los monomios y utilizando la propiedad de la potenciación Ejemplo Dados P(x) = 2x 2 – 5x 2 y Q(x) = 3x 2 x Realizar P(x)



2




Equivalencias Logicas Proyecto P V Q P Q Mp4 Youtube
P« q p si y sólo si q p « q p es condición necesaria y suficiente para q p « q p es condición para q y q es condición para p p« q si p entonces q y si q entonces p El valor de verdad del bicondicional es verdadero cuando ambas proposiciones son verdaderas o cuando ambas son falsas 5 Polinomios Booleanos o fórmulasP, Q y Q' 2º Trazamos la circunferencia P O Q Q' P O Q Q' P P' La potencia es una propiedad de un punto respecto a una circunferencia, es una relación concreta La inversión es una transformación que se puede poner en práctica con cualquier punto en el plano una vez queda determinada la constante de la inversión3 EJERCICIO 607 Comprobar por tablas de verdad si las siguientes fbfs son o no simultáneamente satisfa cibles ¬(p → q) p ∨ q p q ¬(p → q) p ∨ q V V F V V F V V F V F V F F F F Las dos fbfs son simultáneamente satisfacibles, ya que son V a la vez en la 2ª interpre tación EJERCICIO 608 Comprobar por tablas de verdad si las siguientes fbfs son o no simultáneamente satisfa



1 Proposiciones Lgicas La Lgica Proposicional O Tambin




Ppt Capitulo I Powerpoint Presentation Free Download Id
Y el tercer argumento, a pesar de no ser válido, se puedeP → q, p ├ q El condicional o implicación es aquella operación que establece entre dos enunciados una relación de causaefecto La regla 'ponendo ponens' significa, "afirmando afirmo" y en un condicional establece, que si el antecedente (primer término, en este caso p) se afirma, necesariamente se afirma el consecuenteSi P es falso, entonces la proposición P, Q es verdadera independientemente del valor de Q Por tanto, P si los valores de las variables que hacen a P verdadero también hacen verdadero a Q De manera equivalente P Q significa que P y Q no tienen nunca de manera simultánea los valores de verdad 1 y 0 respectivamente




Ejerc N 14 Unt 17 Disyuncion Exclusiva Youtube




Departamento De Formacion General Ppt Video Online Descargar
Proposiciones Llamaremos proposiciones a aquellas frases del lenguaje natural, las cuales podamos afirmar que son verdaderas o falsas Ejemplos de proposiciones Dos es par Tres es mayor que diez Tres más cuatro es nueve 3 Una proposición es simple o atómica, si ninguna parte de ella es a su vez una proposiciónNota 1La única manera que puede ser falsa p→q es si p es verdadera y q es falsa—esto es el caso de la "la promesa rota" 2Si estudias la tabla de verdad una vez más, puedes ver que decimos que "p→q" es verdadera cuando p es falsa, sin importa el valor de verdad de qPropiedades de las operaciones lógicas Va mos a examinar las propiedades que tienen las operaciones lógicas antes definidas, para ello consideramos que p, q y r son tres proposiciones cualesquiera Entonces tenemos los siguiente Como la proposición se simplifica al valor de verdad (V), ésta es una tautología




Corregimos Las Inversiones Q P Y D B Pictogramas Arasaac Actividades Para Dislexia Lectoescritura Actividades



2
Capítulo I Lógica proposicional 3 13 Operadores lógicos Negación Dada una proposición p su contraria no p es verdadera cuando aquella es falsa y se simboliza ¬p p ¬p 0 1 1 0 Conjunción o producto lógico Dadas dos proposiciones p, q, el producto lógico es la proposición molecular p y q que se simboliza (p ∧ q) p q p ∧ q 0 0 0Q ^r)!(p !(q ! 1) "p→q" 的意思是: 如果p为真,则必推出q为真; 如果p为假,则q可能为真或假(q不必然为假); 2)"非p 或 q" 的意思可以分为三种情况: a)非p为假而q为真;即,p真且q真; b)非p为真而q为真;即,p假且q真; c)非p为真而q为假;即,p假且q假



Eur Lex Europa Eu




Pdf Une Etude Comparative De L Enseignement Du Calcul Algebrique En France Et Au Chili
10 4 Escribe cada uno de los siguientes estamentos en la forma si p, en tonces q a) Nieva siempre que el viento sopla del noroeste Si el viento sopla del noreste, entonces nieva b) Que el Depor gane la liga, implica que ha derrotado al Real Madrid Si elLa condicional P → Q es la proposición que dice que si P es cierta entonces Q también es cierta, se lee "si P entonces Q" Ejemplos L n es múltiplo de 4 M n es par L → M Si n es múltiplo de 4 entonces n es par (verdadera) M → L Si n es par entonces n es múltiplo de 4 (falsa) Observar que P → Q no dice que P o Q sean verdaderas, únicamente dice que si P es verdaderaFilosofía y Ciudadanía – Lógica proposicional Ejercicios resueltos 3 5 Enlaza cada proposición con su formalización "Llueve" = p, "Hace sol" = q, "Las brujas se peinan" = r 1 Llueve y hace sol 1A p ∧∧∧∧ q 2 No es cierto que si llueve y hace sol las brujas se peinan 3B r ↔ (p ∧∧∧∧q) 3 Las brujas se peinan únicamente si llueve y hace sol 4C ¬r → ( ¬p



2




Propiedades De Los Numeros Reales Ppt Descargar
∂p ∂q ∂f = ∂t H, f where H, f = ∂H ∂p ∂f ∂q ∂H ∂q ∂f ∂p So, if f is conserved and not an explicit function of time, its Poisson bracket with H is zero df ∂f ∂f H, f = , so if = 0 dt ∂t ∂t df then H, f = 0 ⇐⇒ = 0 dt This must mean that q is false and p ∧ ( p → q) is true (if we want A → B to be false, we need A true and B false) Hence both p and p → q are true But this gives q true, which is a contradiction This technique is particularly slick for three'variable' statements as it saves you doing a giant 8row truth table




Formalizacion De Proposiciones Pdf




Consistencia E Inconsistencia Pdf



2



2



2



Matematica I Calameo Downloader




Propiedades



2



2



2




Carlos M Madrid Casado Teoria Del Cierre Categorial Aplicado A La Mecanica Cuantica I El Catoblepas




Circuitos Logicos Conmutadores Y Compuertas P Qvr




P Q P R



Propiedades




Logica Conjuntos Relaciones Y Funciones Pdf Descargar Libre




Algebra De Proposiciones Pdf Proposicion Validez



Quantun Electronics Llc Qp 750 Download Online Gratis Brugs Og Vedligeholdelsesvejledning




U1 Leyes Logica Pdf




Si Socrates Es Un Ser Humano Entonces Socrates Es Mortal Socrates Es Un Ser Humano Pdf Free Download




Apunte Udec Algebra Lineal Pdf Txt




Ppt 1 1 La Recta Numerica Powerpoint Presentation Free Download Id




Guia 1 Complementos Mat021 Pdf Docer Com Ar



C Con Clase Curso De Graficos Ape2




Segmento De Recta Formulas Matematicas Geometria Analitica Partes De La Misa



2




Les Loisirs D Un Etranger Au Pays Basque 1901 Pdf Basques Voyage En Europe




Mundo Preuniversitario Matematika Mathematique Mathematics Physics Fizika Shahmaty Teoria De Los Conjuntos Prof Carlos Ivorra Castillo




Captulo I Lgica Y Conjuntos Temas Del Captulo




Ppt Departamento De Powerpoint Presentation Free Download Id



2




Propiedades De Los Numeros Reales Ppt Video Online Descargar



Lya Fciencias Unam Mx



2




Vectores




Espacio Afin Apuntes De Matematicas Docsity



I 1bgu M Pg239 Ej8 A Youtube




Leyes Logicas Ejercicios Resueltos De Algebra Proposicional Pdf En 21 Ejercicios Resueltos Algebra Conmutativa




Propiedades De Potencia Y Ecuaciones Exponenciales Pdf



2




3 Algebra Vectores 11 Pdf




Inteligencia Artificial Ia 7700 T M C Juan




Capitulo I Logica Y Conjuntos Ppt Descargar




Ley Conmutativa En Tablas De Verd By Kevin Villarraga




Tema 4 Propiedades De Los Numeros Reales




Formulario Y Ejercicios Resueltos



Unidad 1 Logica Y Conjuntos Pdf Free Download




P Q P R




Matematicas Discretas Ppt Descargar




Modulo Vectores




Ley Conmutativa En Tablas De Verd By Kevin Villarraga




Apuntes



Inteligencia Artificial Ppt Descargar



Segmentos Dirigidos Matetam




Conjunto Relaciones Funciones Y Logica Pdf Free Download




Resumen Mad Cuatrimestre Completo Onenote Matematica Discreta Ingenieria En Sistemas De Informacion Utn Filadd




Letra Qp Fotos E Imagenes De Stock Alamy




M I C Hector E Medellin Anaya Ppt Descargar




Simplificacion De Proposiciones Logicas 1 Matematica Youtube




Propiedades




Logica Proposicional Ing Nerio Villalobos Finol Pdf Free Download




Leyes Logicas Ejercicios Resueltos De Algebra Proposicional Pdf En 21 Ejercicios Resueltos Algebra Conmutativa




Transformaciones Geometricas




Ejercicios De Simplificacion De Ecuaciones Logicas 1 Maatematicas Studocu




Fisica Ensenanza Y Curiosidades La Ecuacion De Max Born



Las Formas Del Pensamiento Calameo Downloader



2




Pdf Propiedades Mecanicas De Nitruros Metalicos Depositados Con Ubm Tecnologia Eficiente Y Ambientalmente Limpia




Tablas De Verdad Ejercicio 3 Youtube




1 Introduccion El Cuerpo De Los Numeros Racionales Pdf Descargar Libre




Propiedades Metricas Apuntes Geometria Propiedades Propiedades De Dos Rectas El De Dos Rectas R Studocu




Fisica Ensenanza Y Curiosidades La Ecuacion De Max Born




Ejemplo Mostrar Que P Q V F Ppt Descargar


