SOLUTION 15 Since the equation x 2 xy y 2 = 3 represents an ellipse, the largest and smallest values of y will occur at the highest and lowest points of the ellipse This is where tangent lines to the graph are horizontal, ie, where the first derivative y'=0Rewrite the equation as − 3 2 x 2 = 0 3 2 x 2 = 0 − 3 2 x 2 = 0 3 2 x 2 = 0 Add 3 2 3 2 to both sides of the equation x 2 = 3 2 x 2 = 3 2 Since the expression on each side of the equation has the same denominator, the numerators must be equal x = 3 x = 3 Multiply both sides of the equation by 2 2Graph 2y^2x^22x8y3=0 Find the standard form of the hyperbola Tap for more steps Subtract from both sides of the equation Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola
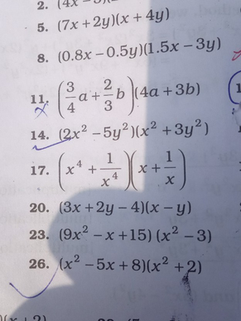
2 14x 5 7x 2y X 4y 8 0 8x 0 5y 1 5x 3y 11 Scholr
(x^2 y^2 - 0.8)^3 = x^2y^3
(x^2 y^2 - 0.8)^3 = x^2y^3-Lets rewrite the equation as below mathp(x,y)dxq(x,y)dy=0/math mathp(x,y)=xy^3y/math mathq(x,y)=2(x^2y^2xy^4)/math The equation is called exact2nd y=2x3Rewrite 2nd as follows 3rd 2xy=3 Multiply 1st by 2 to get 4th 2x4y=0 Subtract 4th from 3rd to get 5th 3y=3 y=1 Substitute this value into 1st to solve for x x2(1)=0 x=2 Solution (2,1) Cheers, Stan H



Solve The Following Pair Of Linear Equations By Substitution Method 3x 2y 7 0 4x Y 6 0 Sarthaks Econnect Largest Online Education Community
Answer to 1) If X^2y^3=4/27 and dy/dt=1/2 , then what is dx/dt This problem has been solved!3132 f(x;y)=œ xy(x2−y2) x2y2 (x;y)≠(0;0) 0 (x;y)=(0;0) Note fis continuous, (by computing lim(x;y)→(0;0) of the formula above, eg using polar coorinates) (a) Find f x and f y when (x;y)≠(0;0) Away from (0;0);fcan be di erentiated using the formula de ning it, as @f @x (x;y)= (x2 y2)y(x2 −y2)2x2y−2x2y(x2 −y2) (x 2ySolve the following system of equations by substitution method x/2 y = 08;
I have that on a shirt D The front is "I ((x 2 y 2 1) 3 x 2 y 3 < 0) Henry Sibley math team, and the back is a graph of itBy subsitution method 2x= y x =y/2 Put the value of x in second eqn x 2y3 y/2 2y3=0 y4y6/2=0 87y6=0 7y=14 Y =2 Put he value of y in first eqn 2x3y=8 2x3 (2)=8 2x6=8 2x=86 2x=2 X=1 1 Thank You Jot Virk🍁♠ 2 years, 5 months ago Y=2, X=1 1 Thank You Honey 😊😊😊 2 years, 5 months ago X=1 and y=2Use calculus to find the area bounded by the circle x^2y^22x2y23=0 and the pair of lines x^22xyy^27x7y12=0 Use calculus to find the area bounded by the circle x 2 y 2 − 2 x − 2 y − 2 3 = 0 and the pair of lines x 2 2 x y y 2 − 7 x − 7 y 1 2 = 0
Solve Homogeneous Differential Equation ProblemsSystemofequationscalculator x2y=2x5, xy=3 en Related Symbolab blog posts High School Math Solutions – Systems of Equations Calculator, Nonlinear In a previous post, we learned about how to solve a system of linear equations In this post, we will learn howJustAnswer is not responsible for Posts




College Algebra In Context 5th Edition Harshbarger Solutions Manual




1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y
Δ = b 24ac Δ = 16 24·2·0 Δ = 256 The delta value is higher than(x^2 y^21)^3 x^2y^3 = 0 WolframAlpha April 21 Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionalsX2 2y2 = lim x!0 0 x2 = 0 Approaching (0;0) along the yaxis (x = 0), lim (x;y) !(0;0) 2xy x2 2y2 = lim y 0 0 2y2 = 0 Approaching (0;0) along the line y = x, lim (x;y)!(0;0) 2xy x2 2y2 = lim x!0 2x2 3x2 = 2 3 The limit does not exist Example Find the limit lim (x;y)!(0;0) x2y x4 y2 if it exists Approaching (0;0) along the line y




Mathematics Mathematics For Economics An




Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 2 3 By Ayman Alam Issuu
Solve on {eq}(0,\infty) {/eq} {eq}x^2y''xy'(x^2\frac{1}4)y=x^{\frac{3}2} {/eq} Given two solutions to the associated homogeneous differential equationX 2 y 2 − 1 = x 2 / 3 y , which can easily be solved for y y = 1 2 ( x 2 / 3 ± x 4 / 3 4 ( 1 − x 2)) Now plot this, taking both branches of the square root into account You might have to numerically solve the equation x 4 / 3 4 ( 1 − x 2) = 0 in order to get the exact x interval Share answered Dec 22 '12 at 1731 Christianマーキー 生き残ります 換気 X 2 Y 2 1 3 X 2y 3 0 Gaia Co Com For more information and source, see on this link http//wwwgaiacocom/x2y213x2y30



Www Researchgate Net Profile Mohamed Mourad Lafifi Post How Can Add A New Method To The Solver Of Simulink Attachment 5a355b1fb53d2f0bba44d1f8 As 3a Download Solving Differential Equations Using Simulink Pdf



The Glop Linear Solver Or Tools Google Developers
It is x2y3 =0 which is of the form AxByC =0 and is the general form of equation to a straight line x2y=3 implies x3 = 2y Dividing by 2 (1/2)x (3/2) = y That is y = (1/2)x (3/2) which is the slope and yintercept form of the line When the coefficient of y is 1 on one side of the equation,the coefficient of x on the other side3 Solution (ex siny 3y)0 y = e x cosy 3 ¡(3x¡ex siny)0 x = ¡3e x siny That is the differential equation is not exact 7 (yexy cos2x¡2exy sin2x2x)dx(xexy cos2x¡3)dy = 0Solution (yexy cos2x¡2exy sin2x2x)0y = e xy cos2xxyexy cos2x¡2xexy sin2x (xexy cos2x¡3)0x = e xy cos2xxyexy cos2x¡2xexy sin2x Thus, the differential equation is exact Then, Z (xexy cos2x¡3Answer to Solve initial value problem y''2y'2y=0, y(0)=8, y'(0)=3 By signing up, you'll get thousands of stepbystep solutions to your




X 2 Y 2 1 3 X 2y 3 0 Novocom Top




Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3
Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method 2x2y=2;3x2y=12 Tiger Algebra Solver3x2y=2;2xy=8 Simple and best practice solution for 3x2y=2;2xy=8 Check how easy it is, to solve this system of equations and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework X2y=8 3x2y=6 Answered by a verified Math Tutor or Teacher Disclaimer Information in questions, answers, and other posts on this site ("Posts") comes from individual users, not JustAnswer;



Silo Tips Download Chapter 13 Solving Simultaneous Equations




Solutions To Problems In Chapter One Mathematics
Not a problem Unlock StepbyStep Extended Keyboard ExamplesClick here👆to get an answer to your question ️ Coordinates of the centre of the circle which bisects the circumferences of the circles x^2 y^2 = 1 x^2 y^2 2x 3 = 0 and x^2 y^2 2y 3 = 0 isStep 1 The trick is to make the change of (independent) variable t = ln x, to reduce the equation to a linear differential equation with constant coefficients, which presumably you already know how to solve Then x = e^t and dt/dx = 1/x If you a




Matlab Tutorial




X 2 Y 2 1 3 X 2y 3 0 Novocom Top
How do you place 02, 022, 0222, , and on a numberY2 x 4 volume = Z 2 22 Z 4 y 1x2y2 dx dy = Z 2 2 x x3 3 y2 4 y2 dy = Z 2 2 4 64 3 y2 y2 (y )3 3 y2 dy = Z 2 2 y8 3 61 3 y2 4 dy = y9 27 61 9 y3 4y 2 2 = 2336 27Giải hệ x^2y^2xy=1 và x^3y^3=x3y Giải hệ PT { x2 y2 xy = 1 x3 y3 = x 3y { x 2 y 2 x y = 1 x 3 y 3 = x 3 y Theo dõi Vi phạm YOMEDIA




Matlab Tutorial




X 2y Y 2 0 Novocom Top
Use the method of separation of variables if x ≠ 0 and y ≠ 0 (note that y = 0 is a stationary solution) then x = − ( 1 y 2) y 3 ⋅ y ′ = ( − 1 y 3 − 1 y) ⋅ y ′ which implies that x 2 2 = ∫ x d x = ∫ ( − 1 y 3 − 1 y) d y = 1 2 y 2 − ln y C Therefore a solution y ( x) satisfies the equation x 2 Sketch the area between two curves and then find the area This is using summations y=2x 1/3, y= (1/8)x 2, 0Putting x = 4, we get y = 5 Thus, we have the following table for the equation 3x 2y – 2 = 0 Now, plot the points P (0, 1) and Q (4, 5) The point C (2, 2) has already been plotted Join PC and QC and extend it on both ways Thus, PQ is the graph of 3x 2y – 2 = 0 The two graph lines intersect at A (2, 2)



X Y Z Geqslant 0 X Y 2 Z 3 1 Prove X 2y Y 2z Z 2x Frac12 Mathematics Stack Exchange




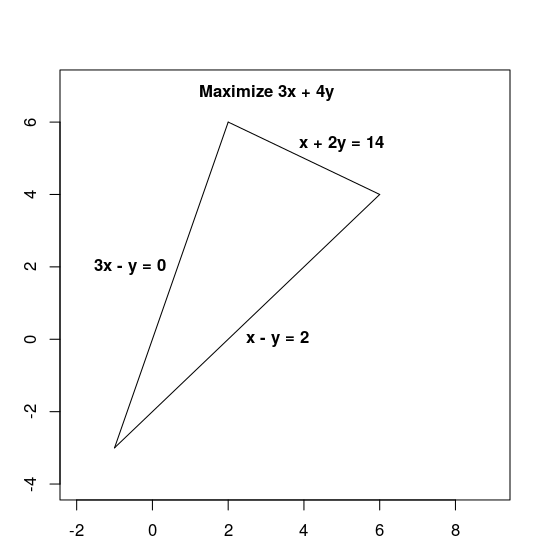
Solve The Following System Of Inequalities Graphically X 2y Less Than Or Equal To 3 3x Plus 4y Greater Than Or Equal To 12 X Greater Than Or Equal To 0 Y
2(xy)(x2y)^2 Both terms are multiple of (x2y)^2, so we can collect it 3x(x2y)^2 (x2y)^3 = (x2y)^2 3x(x2y) Simplifying the square brackets gives 3x(x2y) = 3xx2y = 2x2y=2(xy) So, the whole expression equals 2(xy)(x2y)^2X y/2 = 7/10 asked in Linear Equations by Anika01 ( 571k points) pair of linear equations in two variables Transcript Example 7 Solve the following pair of equations by substitution method 7x – 15y = 2 x 2y = 3 7x – 15y = 2 x 2y = 3 From (1) 7x – 15y = 2 7x = 2 15y x = (𝟐 𝟏𝟓𝒚)/𝟕 Substituting the value of x in (2) x 2y = 3 (2 15𝑦)/7 2𝑦=3 Multiplying both sides by 7 7 × ((2 15𝑦)/7) 7×2𝑦=7×3 (2 15y) 14y = 21 15y 14y = 21 – 2 29y = 21 – 2




Matlab Tutorial



Solve The Following Systems Of Equations X 2 Y 0 8 Sarthaks Econnect Largest Online Education Community
Solve Quadratic Equation by Completing The Square 52 Solving x26x5 = 0 by Completing The Square Subtract 5 from both side of the equation x26x = 5 Now the clever bit Take the coefficient of x , which is 6 , divide by two, giving 3 , and finally square it giving 9 Add 9 to both sides of the equation On the right hand side we haveUnlock StepbyStep (x^2y^21)^3x^2y^3=0 Extended Keyboard ExamplesFree PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep
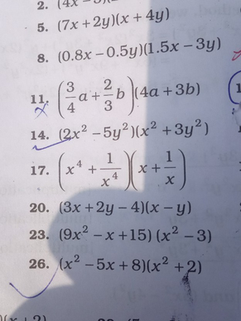



2 14x 5 7x 2y X 4y 8 0 8x 0 5y 1 5x 3y 11 Scholr




With Modelling And Visualization 3 E Ppt Download
Find the volume of the given solid under the surface z = 1 x2y2 and above the region enclosed by x = y2 and x = 4 (x;y) is in the region , 2 y 2;Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreX 2 Y 2 1 3 X 2y 3 0 Wolfram Alpha Wolfram Alpha Mathematics For more information and source, see on this link https//wwwpinterestcom/pin//




Ml Aggarwal Cbse Solutions Class 7 Math Fifth Chapter Algebraic Expressions Exercise 5 1



Http Gpsbulldogmath Weebly Com Uploads 8 7 0 6 Chapter 10 Book Answer Keys Pdf
94CEMATHS II 8 94 39 If x = 3, y = 2 satisfy the simultaneous equations 3 2 bx ay ax by, find the values of a and b A a = 0, b = 1 aB = 0, b = 1 C a = 6 5, b = 4 1 D a = 13 1 , b = 39 37 E a = 13 12 , b = 13 5 94 40 From the table, which of the following y = x 2 and substituting this into the first equation, we have x^2 (x 2)^2 = 8 expand and simplify x^2 (x^2 4x 4) = 8 x^2 x^2 4x 4 = 8 4x 4 = 8 add 4 to both sides 4x = 12 divide by 4 x = 3 And, since y = x 2 we have y = 3 2 = 1 Soour solution is (3, 1)Click here👆to get an answer to your question ️ Find the centre and radius of the circle x^2 y^2 x 2y 3 = 0



Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf




Systems Of Linear Equations Ppt Download
Solution for X^2y^2=18;X2y=3 equation X^2X^2=18X2X=3 We move all terms to the left X^2X^2(18X2X)=0 We add all the numbers together, and all the variables X^2X^2(16X)=0 We add all the numbers together, and all the variables 2X^2(16X)=0 We get rid of parentheses 2X^216X=0 a = 2;Plot (x^2y^21)^3x^2y^3=0 WolframAlpha Rocket science?Check to see if f y is equal to N f y = −x 2g0(y) = 6y −x2 3 so that g0(y) = 6y2 3 That gives g(y) = 2y3 3y Put this back in to get the full solution, f(x,y) = c x3 −x2y 2x2y3 3y = C 3 Problem 4 (2xy2 2y)(2x2y 2x)dy dx = 0 Check for "exactness"




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Solve The Following System Of Equations X 2 Y 0 8 7 X
See the answer See the answer See the answer done loading1y=16(25)^x 2y=08(128)^x 3y=17(1/5)^x'' How do I determine if this equation is a linear function or a nonlinear function? Explanation From the given equation x2 y2 2x −3 = 0 perform completing the square method to determine if its a circle, ellipse, hyperbola There are 2 second degree terms so we are sure it is not parabola x2 y2 2x −3 = 0 x2 2x y2 = 3
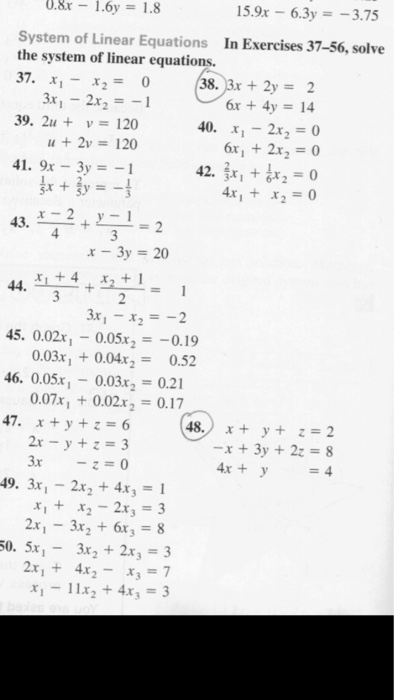



System Of Linear Equations In Exercises 37 56 Solve Chegg Com
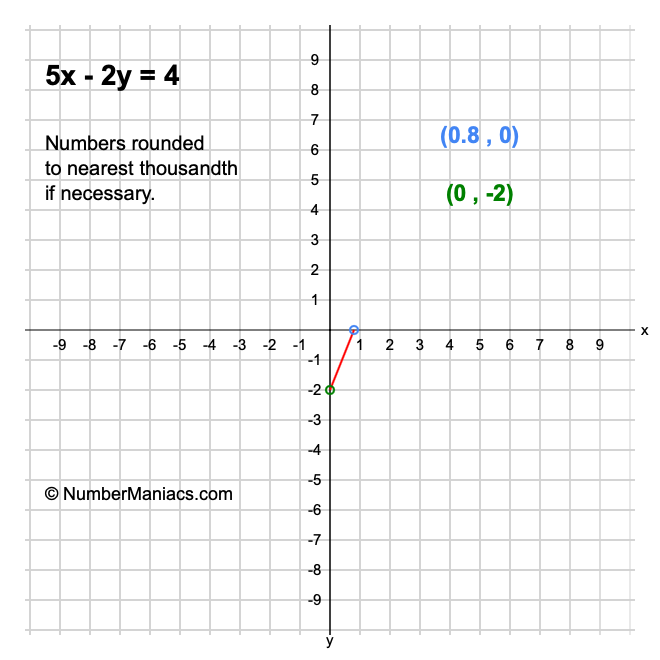



5x 2y 4
Solve the differential equation (x^2 4xy 2y^2)dx (y^2 4xy 2x^2)dy = 0 asked in Differential equations by AmanYadav ( 556k points) differential equations The solution of the set of equations x2y=3 and 2xy=6 has to be determined One way of doing this is to actually solve the given set of equations



1




Kseeb Sslc Class 10 Maths Solutions Chapter 3 Pair Of Linear Equations In Two Variables Ex 3 2 Kseeb Solutions




Solutions Manual For Basic College Mathematics 12th Edition By Bittin




C H A P T E R 7 Manualzz



Www Sgasd Org Site Handlers Filedownload Ashx Moduleinstanceid 9221 Dataid Filename Answer key Pdf




Solved Example Problems For Regression Analysis Maths




Introductory Mathematical Analysis Textbook Solution Manual




X 2 Y 0 8 7 X Y 2 10




Practice Your Skills For Chapter 3 Pdf




X 2 Y 0 8 And 7 X Y 2 10 Brainly In




Solve The System Of Equations Frac X 2 Y 0 8 And Frac 7 X Y 2 10 And Also Find The Value Of Frac X Y Snapsolve




0 4x 0 3y 1 7 0 7x 0 2y 0 8 7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 X Y 2 4 X 3 2y 5 Solve This In Two Min From Substitution Elimination And Cross Multiplication Method Edurev Class 10 Question



Mathscene Vectors Lesson 5




Keep Calm And X 2 Y 2 1 3 X 2y 3 0 You Poster Boronuraniumnitrogengallium Keep Calm O Matic




Solve For X Y X 2 Y 0 8 7 X Y 2 10 Brainly In




Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3



What Is The Equation Of Tangent To Circle X Y 6x 4y 3 0 Which Is Perpendicular To Line Y 2x 1 Quora




Mathematics For Economics Business 5th Ed 06 Ian Jacques




0 4x 0 3y 1 7 And 0 7x 0 2y 0 8 By Elimination Method Brainly In




0 4x 0 3y 1 7 0 7x 0 2y 0 8




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




If The Equation Kx 2y 5 3x Y 1 Has No Solution Then What Is The Value Of K Quora




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Solutions Manual For Intermediate Algebra 8th Edition By Tobey Ibsn 9




Solve For X Y X 2 Y 0 8 7 X Y 2 10 Brainly In



Solve The Following Pair Of Linear Equations By Substitution Method 7x 15y 2 X 2y 3 Sarthaks Econnect Largest Online Education Community




Chapter P Prerequisites Manualzz




X 2 Y 2 0 8 3 X 2 Y 3 Naukas




Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 2 3 By Ayman Alam Issuu




Pdf Chap Sushant Singh Academia Edu




Numerical Methods In Engineering With Matlab




Pdf Partial Derivatives 13 1 Functions Of Several Variables Joseph Feliz Academia Edu




Using Cramer S Rule In Exercises 9 22 Use Cramer S Chegg Com



Solve The Following Pair Of Linear Equations By Substitution Method 3x 2y 7 0 4x Y 6 0 Sarthaks Econnect Largest Online Education Community




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Solde The Following Systems Of Equations 1 11x 15y 23 0 7x 2y 0 3 0 4x 0 3y 1 7 0 7x 0 2y 0 8 5 7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 9 4 2y 5
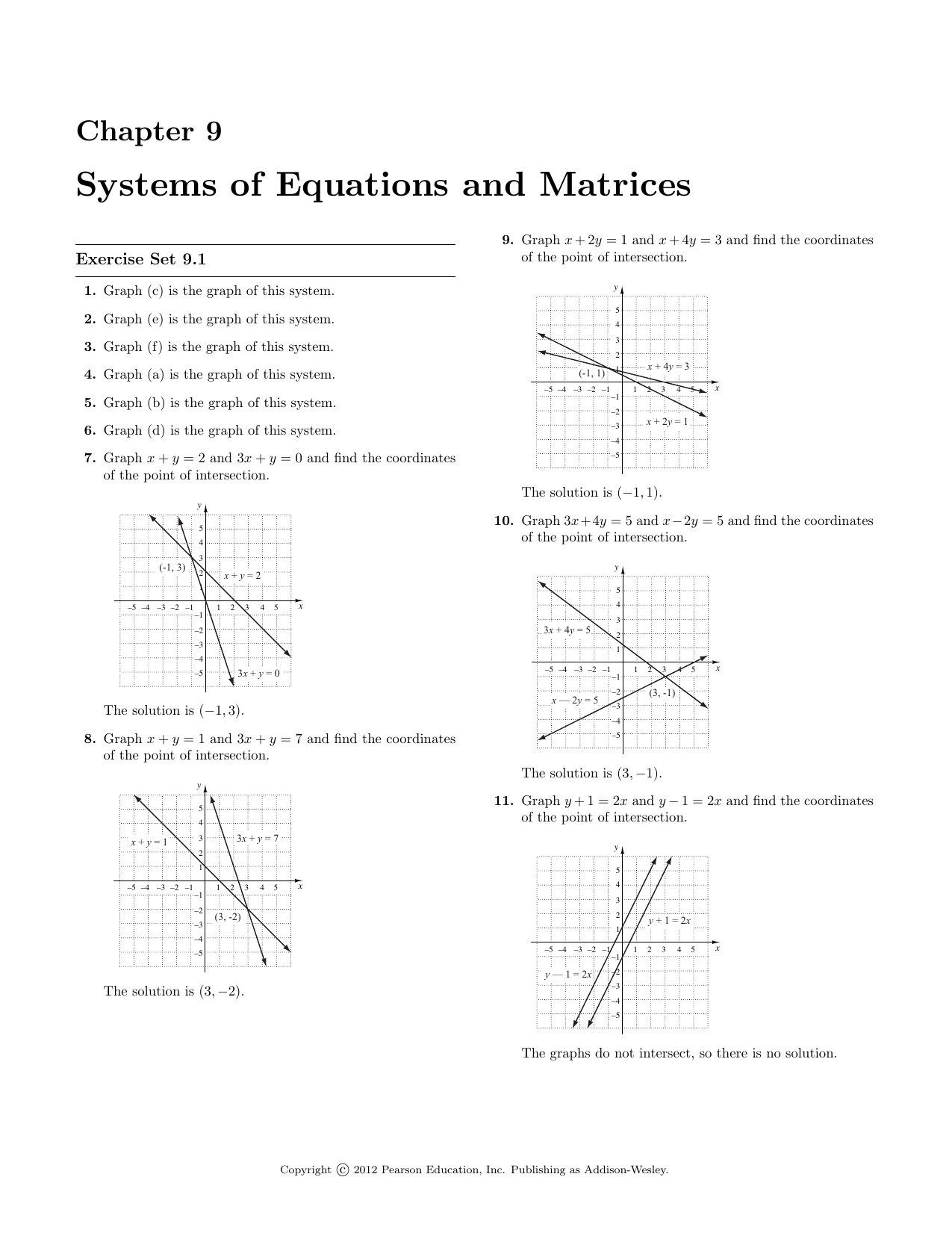



Chapter 9 Systems Of Equations And Matrices Manualzz
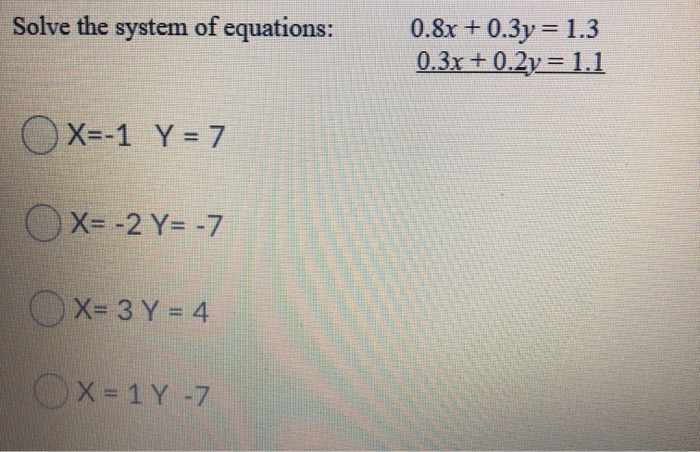



Solve The System Of Equations 0 8x 0 3y 1 3 0 3x Chegg Com




If X 2 Y 0 8 And 7 X Y 2 10 Find X Y Brainly In




Numerical Methods




Solved Example Problems For Regression Analysis Maths



1




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Solve For X And Y X 2 Y 0 8 X Y 2 0 7 Brainly In



Pycse Python3 Computations In Science And Engineering




11x 15y 23 0 And 7x 2y 0 Solve Using Substitution Method Youtube




Linear Equations Questions And Answers Topperlearning




Pair Of Linear Equations In Two Variables Class 10 Solutions Exercise 3 3




Pair Of Linear Equations In Two Variables Class 10 Solutions Exercise 3 3
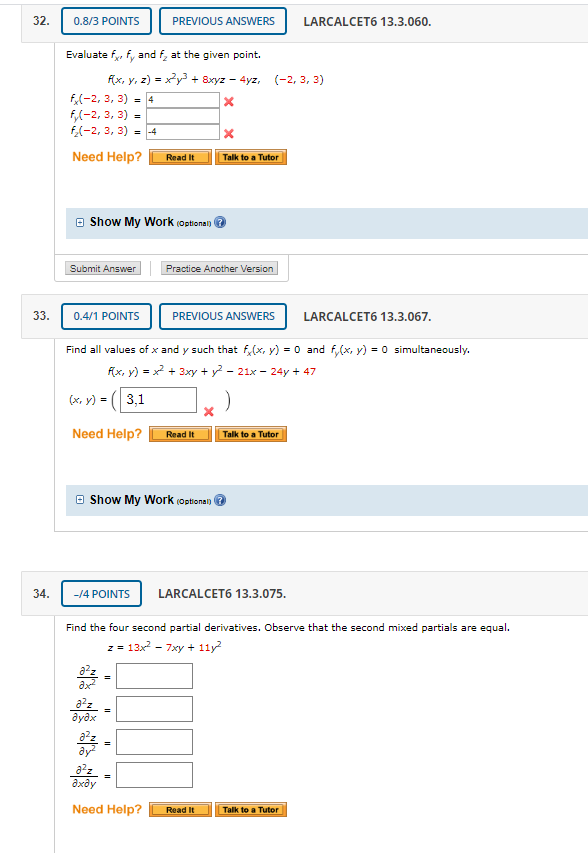



32 0 8 3 Points Previous Answers Larcalcet6 Chegg Com



1




Plotting X 2 Y 2 1 3 X 2 Y 3 0 Mathematics Stack Exchange




3 Systems Of Linear Equations



Www Home Uni Osnabrueck De Mfrankland Math241 Math241 163 Conservative Pdf



Www Researchgate Net Profile Mohamed Mourad Lafifi Post How Can Add A New Method To The Solver Of Simulink Attachment 5a355b1fb53d2f0bba44d1f8 As 3a Download Solving Differential Equations Using Simulink Pdf
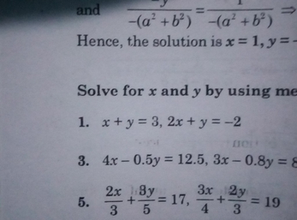



Hence The Solution Is X 1 Y Solve For X And Y By Using Me Scholr




Systems Of Linear Equations Ppt Download
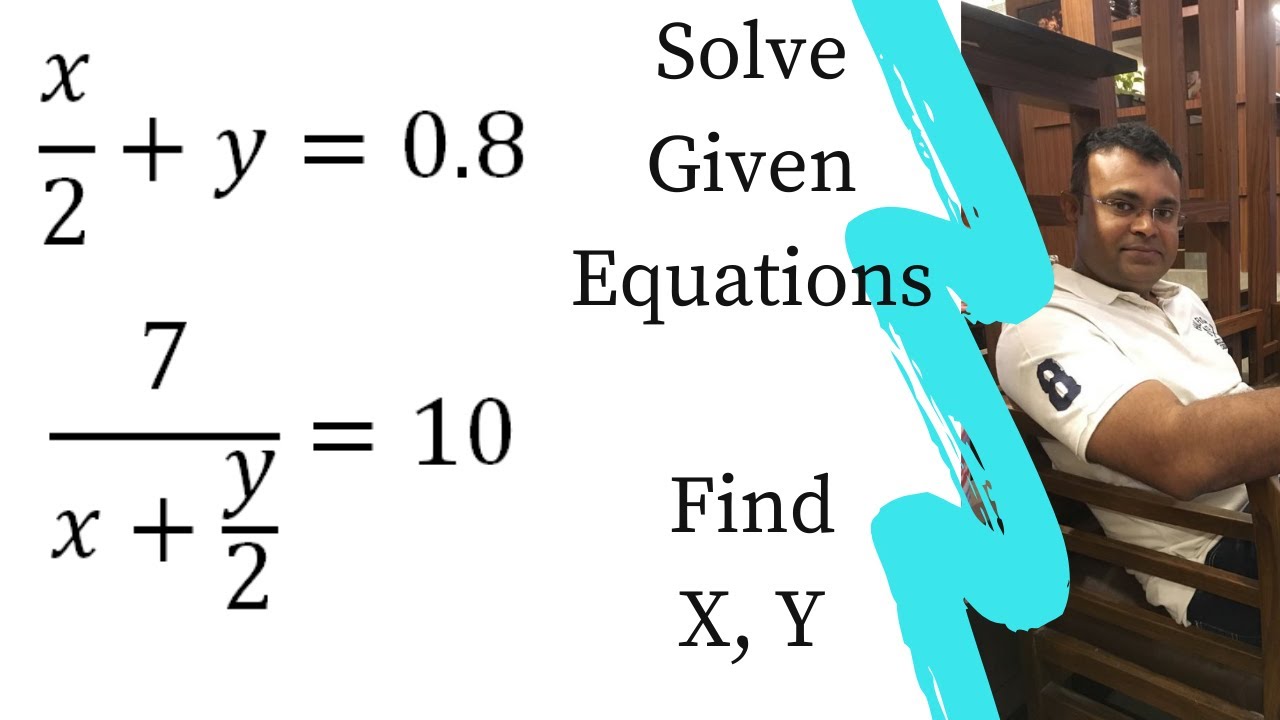



Solve X 2 Y 0 8 7 X Y 2 10 Youtube




Doc Chapter Four Derivatives Of Multivariate Functions Partial Differentiation Habtamu Destaw Academia Edu




Ml Aggarwal Cbse Solutions Class 7 Math Fifth Chapter Algebraic Expressions Exercise 5 1




X 2 Y 1 2 Hence Le Solde The Following Systems Of Equations 1 11x 15y 23 0 7x 2y 0 3 0 4x 0 3y 1 7 0 7x 0 2y 0 8 5 7 Y 3 2 X 2 14 4 Y 2 3 X 3 2




Mathematics For Economics And Business 6th Edition Jacques Solutions Manual By Russell Issuu




Ontario Tech University Engineering Photos Facebook




X 2 Y 0 8 And X Y 2 0 7 By Cross Multiplication Solve It



Solve The Following System Of Equations By Substitution Method X 2 Y 0 8 X Y 2 7 10 Sarthaks Econnect Largest Online Education Community




Solve For X And Y 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 12 Solve For X And Y 1 2 V 2y Maths Pair Of Linear Equations In Two Variables Meritnation Com



1




X 2 Y 0 8 7 X Y 2 10 Pls Find The Answer For This In Elimination Method X 7 Y 3 5 X 2 Y 9 6find For This Also Rn Maths Pair Of Linear Equations In Two Variables Meritnation Com



Find An Equation Of The Tangent Line To The Curve Y 3x 2 X 3 At The Point 1 2 Graph The Curve And The Tangent Line Enotes Com



Www Researchgate Net Profile Mohamed Mourad Lafifi Post How Can Add A New Method To The Solver Of Simulink Attachment 5a355b1fb53d2f0bba44d1f8 As 3a Download Solving Differential Equations Using Simulink Pdf




0 4 X 0 3 Y 1 7 0 7 X 0 2 Y 0 8 Youtube




X What Value Of Y Will Make N 1 6 4 Y 0 8 2 Y 3 Equal To 0



Http Www Math Utep Edu Faculty Cmmundy Math 2301 Solution Manual Pdf




Solve The Following System Of Equation For X And Y By Using The Method Of Elimination 0 4x 0 3y Brainly In




X 2 Y 1 2 Hence Le Solde The Following Systems Of Equations 1 11x 15y 23 0 7x 2y 0 3 0 4x 0 3y 1 7 0 7x 0 2y 0 8 5 7 Y 3 2 X 2 14 4 Y 2 3 X 3 2



Finden Sie Die Losung Y X Fur Das Anfangswertproblem 2y 3 Y X 0 Y 4 4 Mathelounge


